[백준 17398] 통신망분할 - #Disjoint Set #Java

https://www.acmicpc.net/problem/17398

17398번: 통신망 분할

 

---

문제분석

시간제한: 1초, 메모리제한: 512MB

1. 시간복잡도 분석

- 통신탑(노드) 개수: 100,000

- 간선의 개수: 100,000

▶O(V*E) (불가), O(V^2) (불가), O(E^2) (불가)

▶O(V), O(E) or log scale로 낮춰야..

 

2. 유형 분석

그래프문제인 것 같긴한데 log scale로 떨어트려야 함.

1) LCA -> 공통조상 찾는 문제는 아님 (※ O(쿼리개수Q * log V))

2) 인덱스트리 -> 구간합 찾는 문제 아님 (※ O(쿼리개수Q * log V))

3) 다익스트라 -> 최단거리 찾는 문제 아님 (※ O(E log V))

4) 위상정렬 -> 그래프가 DAG 형태가 아님 (※ O(V + E))

5) 어떤 "집합"으로 표현가능한 자료구조 -> "Disjoint-Set"

  - find 연산: O(V) (경로압축 X) , O(log V) (경로압축)

  - union 연산: find * 2 -> O(log V)

  ▶ 시간복잡도도 가능

 

---

설계

*이슈1

Union-Find로 한 번 합쳐진 집합은 다시 이전의 합치기 전 집합으로 돌아갈 수 없음 (비가역적). 즉, 분할이 X.

이 문제는 분할문제인데... 어떻게 적용할 수 있을까? 가 첫번째 이슈.

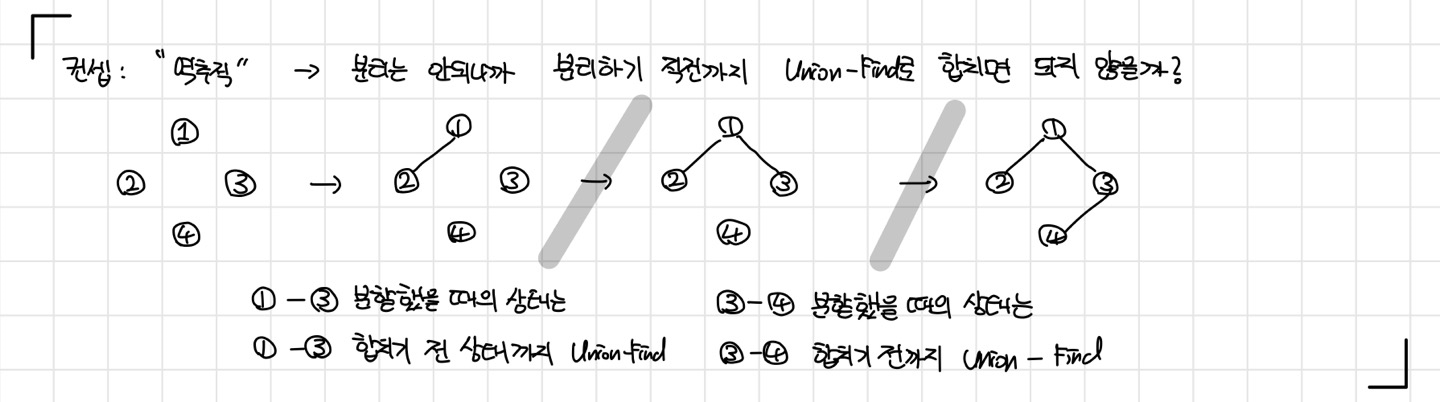
정확히 뭔진 모르겠지만, 뭔가 역추적할 수 있지 않을까? 하는 컨셉을 이해하고 문제에서 주어진 예시를 살펴보자.

 

 

예시

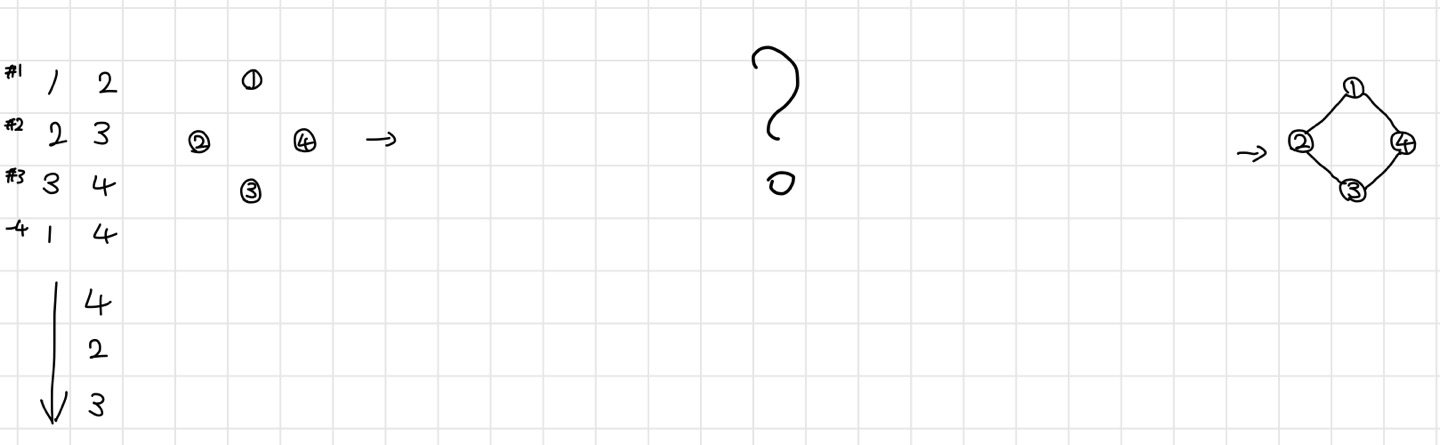
1. Disjoint-Set으로 접근할 것이니, 최초의 서로소 집합의 그래프가 존재할 것이다.

2. #1 ~ #4 번호의 연결정보에 따라 마지막 그래프는 모두가 연결된 그래프의 형태일 것이다.

 

 

 

 

 

 

문제에서 주어진 정보는, "절단 순서와 #1~ #4 번호의 노드정보"이다. 즉, 위의 그림과 같이 그래프를 유추해볼 수 있다.

 

1. #3 절단되었을 때의 비용

#3이 절단이 되었을 때의 그래프를 살펴보자.

#3이 절단되었다는 것은, 3번 노드와 4번 노드가 절단되었다는 것이 확실하다.

 

case1) 3번 노드와 4번 노드가 다른 집합일 경우

비용: 3번 노드 집합의 원소개수(통신망 수) * 4번 노드 집합의 원소개수(통신망 수)

 

case2) 같은 집합일 경우

비용: 0

 

2. #3 절단 비용을 고려했으니, #3 연결 (역추적)

 

3. #2 절단 되었을 때의 비용

...

 

4. 최초상태

절단되지 않은 #i 를 모두 연결한 상태

 

 

이슈1 정리:

 

 

 

---

*이슈2

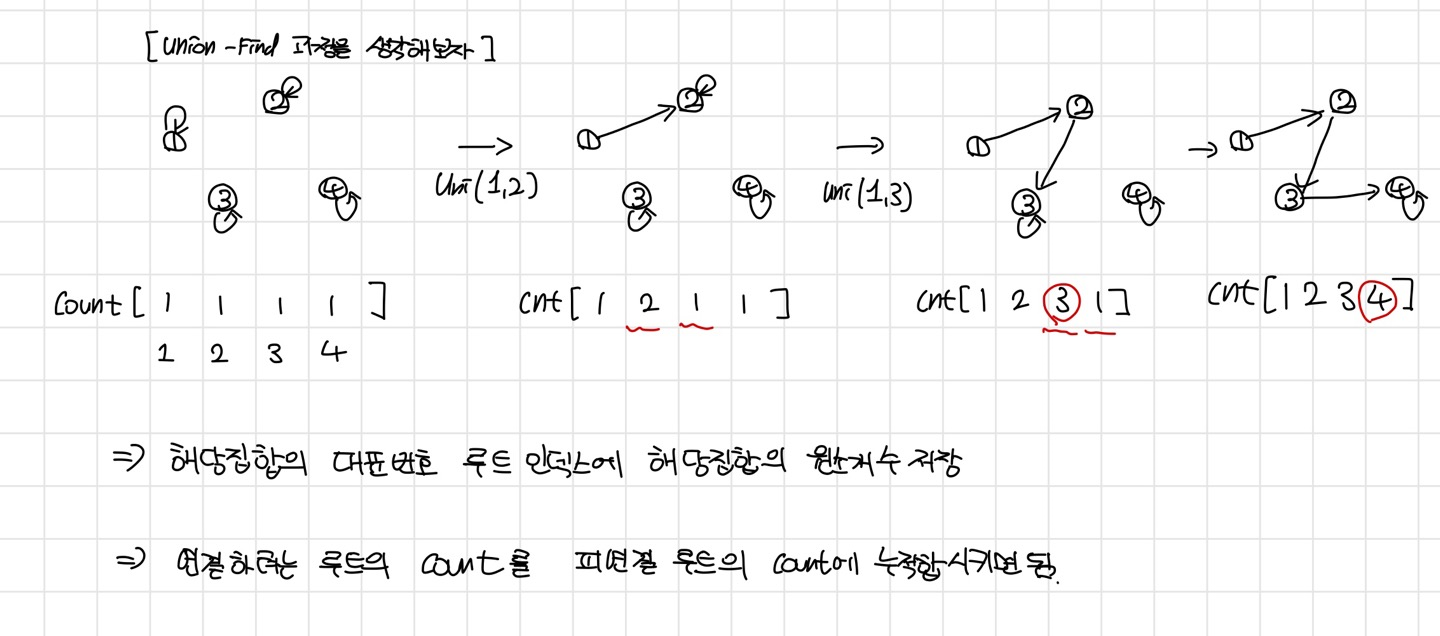
해당 노드가 속한 집합의 원소개수를 어떻게 구하는가?

(★ Union-Find에서 필요한 정보를 들고다니는 테크닉)

 

 

---

코드

public class Main {
	static List<int[]> info;
	static int[] parent;
	static boolean[] notFirst; //최초 시작연결번호를 기록하기 위함
	static Stack<Integer> stack = new Stack<>();
	static int[] count;
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int N = Integer.parseInt(st.nextToken());	//통신망(노드) 개수
		int M = Integer.parseInt(st.nextToken());	//간선 개수
		int Q = Integer.parseInt(st.nextToken());	//간선 분할 횟수
		if(N==1) {
			System.out.println(0);
		} else {
			count = new int[N+1];
			Arrays.fill(count, 1);
			count[0] = 0;
			//parent 자기자신으로 초기화 (서로소 집합)
			parent = new int[N+1];
			for (int i=1; i<=N; i++) {
				parent[i] = i;
			}
			
			info = new ArrayList<>();
			info.add(new int[] {0, 0}); //더미데이터 (idx 1부터 시작하기 위함)
			int a,b;
			for (int i=1; i<=M; i++) {
				st = new StringTokenizer(br.readLine());
				a = Integer.parseInt(st.nextToken());
				b = Integer.parseInt(st.nextToken());
				info.add(new int[] {a, b});
			}
			
			notFirst = new boolean[M+1];
			notFirst[0] = true;
			for (int i=0; i<Q; i++) {
				a = Integer.parseInt(br.readLine());
				notFirst[a] = true;
				stack.add(a);
			}
			
			//최초그래프로 초기화
			for(int i=1; i<=M; i++) {
				if(notFirst[i] == false) {
					union(info.get(i)[0], info.get(i)[1]);
				}
			}
			
			int cut = 0;
			long sum = 0;
			int node1, node2;
			while(!stack.isEmpty()) {
				
				//개수 세고
				cut = stack.pop();
				
				node1 = info.get(cut)[0];
				node2 = info.get(cut)[1];
				
				//다른 집합일 경우만 카운트
				if(find(node1) != find(node2)) {
					sum += 1L * count[find(node1)] * count[find(node2)];	
				}
							
				//연결
				union(info.get(cut)[0], info.get(cut)[1]);
			}
			System.out.println(sum);
		}
	}
	
	
	public static int find(int node) {
		//base case: 루트일 때까지 재귀탐색
		if(parent[node] == node) {
			return node;
		} 
		//recursive case
		return parent[node] = find(parent[node]);
	}
	
	public static void union(int node1, int node2) {
		int aRoot = find(node1);
		int bRoot = find(node2);
		if(aRoot != bRoot) {
			count[bRoot] += count[aRoot];
			parent[aRoot] = bRoot;
		}
	}
}