Union-Find (Disjoint-Set)

Union-Find (Disjoin-Set)

집합들의 정보를 확인(Find)하고 조작(Union)할 수 있는 자료구조

시간복잡도: O(log V) (경로 압축 시)

 

Union-Find 설계

1. 서로소 집합 초기화

자신의 부모가 자기자신을 가리키도록 초기화

for (i: 1 ~ N)
	parent[i] = i

 

2. Find 연산: find (a)

주어진 원소가 속한 집합의 대표번호 (루트) 반환

 

경로 압축 진행 X: O( V ), (가역적)

find(1) -> 2, find(3) -> 4 (parent[3] -> 5)

// O(V)
find (a)
    if parent[a] == a → return a
    else return find(parent[a])

 

 

경로 압축 진행 O: O( log V ), (비가역적)

find(1) -> 2, find(3) -> 4 (parent[3] -> 4)

// O(log V)
find (a)
    if parent[a] == a → return a
    else return parent[a] = find(parent[a])

 

 

3. Union 연산: union (a, b)

a와 b가 속한 집합을 하나로 합치는 연산

* 반드시 집합을 대표하는 번호 (루트)끼리 합칠 것

union (1, 3)

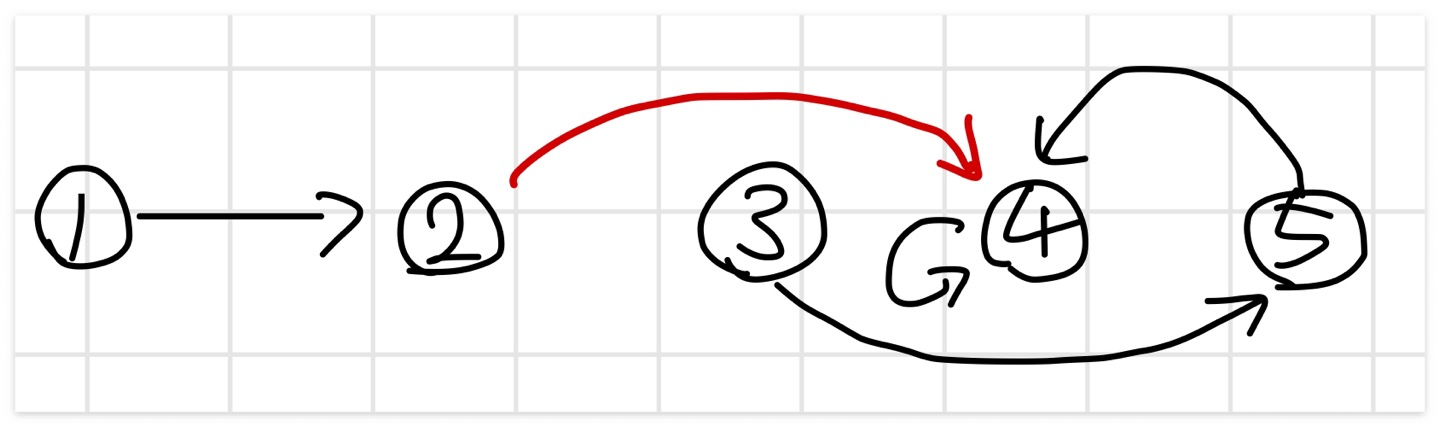
// O(2 * find 연산) → O(2 * log V)
union (a, b)
    rootA = find(a)
    rootB = find(b)
    parent[rootA] = rootB

 

 

---

문제 유형

1. MST (minimum spanning tree)

 

2. 집합의 개수 구하기
https://www.acmicpc.net/problem/11724

• 판단근거: 연결 요소의 개수 == 집합의 개수
  Union 연산으로 집합을 합치고, Find 연산으로 집합의 대표번호 (루트)를 파악한다면 집합의 개수를 파악할 수 있을 것으로 판단